In this tutorial, you'll study merge sort. Also, you'll find working samples of merge sort algorithm in C, C++, Java, and Python.
Merge Sort may be a quite Divide and Conquer algorithm in programming. it's one of the foremost popular sorting algorithms and an excellent thanks to developing confidence in building recursive algorithms.
Using the Divide and Conquer technique, we divide a drag into subproblems. When the answer to every subproblem is prepared, we 'combine' the results from the subproblems to unravel the most problem.
Suppose we had to sort an array A. So we divide this array into subproblems which start at index p and ending at index r, denoted as A[p..r].
Divide
If q is that the half-way point between p and r, then we will split the subarray A[p..r] into two arrays A[p..q] and A[q+1, r].
Conquer
In the conquer step, we attempt to sort both the subarrays A[p..q] and A[q+1, r]. If we've not yet reached the bottom case, we again divide both these subarrays and check out to sort them.
Combine
When the conquer step reaches the bottom step and that we get two sorted subarrays A[p..q] and A[q+1, r] for array A[p..r], we combine the results by creating a sorted array A[p..r] from two sorted subarrays A[p..q] and A[q+1, r].
The MergeSort function repeatedly divides the array into two halves until we reach a stage where we attempt to perform MergeSort on a subarray of size 1 i.e. p == r.
After that, the merge function comes into play and combines the sorted arrays into larger arrays until the entire array is merged.
To sort a whole array, we'd like to call MergeSort(A, 0, length(A)-1).
As shown within the image below, the merge sort algorithm recursively divides the array into halves until we reach the bottom case of array with 1 element. then, the merge function picks up the sorted sub-arrays and merges them to gradually sort the whole array.
Every recursive algorithm depends on a base case and therefore the ability to mix the results from base cases. Merge sort is not any different. the foremost important part of the merge sort algorithm is, you guessed it, merge step.
The merge step is that the solution to the straightforward problem of merging two sorted lists(arrays) to create one large sorted list(array).
The algorithm maintains three-pointers, one for every one of the 2 arrays and one for maintaining the present index of the ultimate sorted array.
A noticeable difference between the merging step we described above and therefore the one we use for merge sort is that we only perform the merge function on consecutive sub-arrays.
This is why we only need the array, the primary position, the last index of the primary subarray(we can calculate the primary index of the second subarray), and therefore the last index of the second subarray.
Our task is to merge two subarrays A[p..q] and A[q+1..r] to make a sorted array A[p..r]. therefore the inputs to the function are A, p, q and r
The merge function works as follows:
b. j maintains a current index of M, starting at 1
c. k maintains the present index of A[p..q], starting at p.
In code, this is able to look like:
A lot is occurring during this function, so let's take an example to ascertain how this is able to work.
As usual, an image speaks a thousand words.
The array A[0..5] contains two sorted subarrays A[0..3] and A[4..5]. allow us to see how the merge function will merge the 2 arrays.
Step 1: Create duplicate copies of sub-arrays to be sorted
Step 2: Maintain a current index of sub-arrays and the main array
Step 3: Until we reach the top of either L or M, pick larger among elements L and M and place them within the correct position at A[p..r]
Step 4: once we run out of elements in either L or M, devour the remaining elements and put in A[p..r]
This step would are needed if the dimensions of M were greater than L.
At the top of the merge function, the subarray A[p..r] is sorted.
Merge sort program in c: -
The space complexity of merge sort is O(n).
Merge Sort may be a quite Divide and Conquer algorithm in programming. it's one of the foremost popular sorting algorithms and an excellent thanks to developing confidence in building recursive algorithms.
Divide and Conquer Strategy for merge sort algorithm
Using the Divide and Conquer technique, we divide a drag into subproblems. When the answer to every subproblem is prepared, we 'combine' the results from the subproblems to unravel the most problem.
Suppose we had to sort an array A. So we divide this array into subproblems which start at index p and ending at index r, denoted as A[p..r].
Divide
If q is that the half-way point between p and r, then we will split the subarray A[p..r] into two arrays A[p..q] and A[q+1, r].
Conquer
In the conquer step, we attempt to sort both the subarrays A[p..q] and A[q+1, r]. If we've not yet reached the bottom case, we again divide both these subarrays and check out to sort them.
Combine
When the conquer step reaches the bottom step and that we get two sorted subarrays A[p..q] and A[q+1, r] for array A[p..r], we combine the results by creating a sorted array A[p..r] from two sorted subarrays A[p..q] and A[q+1, r].
The MergeSort Algorithm
The MergeSort function repeatedly divides the array into two halves until we reach a stage where we attempt to perform MergeSort on a subarray of size 1 i.e. p == r.
After that, the merge function comes into play and combines the sorted arrays into larger arrays until the entire array is merged.
MergeSort(A, p, r):
if p > r
return
q = (p+r)/2
mergeSort(A, p, q)
mergeSort(A, q+1, r)
merge(A, p, q, r)
To sort a whole array, we'd like to call MergeSort(A, 0, length(A)-1).
As shown within the image below, the merge sort algorithm recursively divides the array into halves until we reach the bottom case of array with 1 element. then, the merge function picks up the sorted sub-arrays and merges them to gradually sort the whole array.
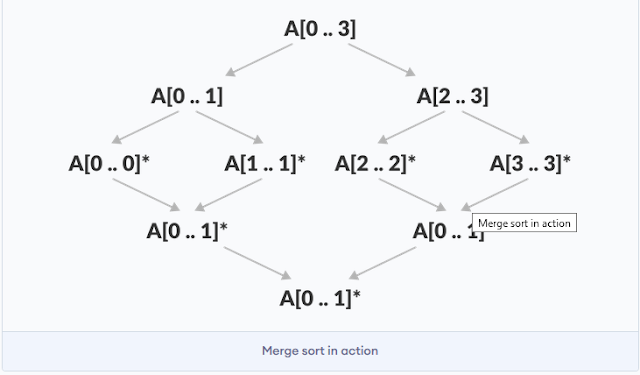 |
| merge sort algorithm |
The merge Step of Merge Sort algorithm
Every recursive algorithm depends on a base case and therefore the ability to mix the results from base cases. Merge sort is not any different. the foremost important part of the merge sort algorithm is, you guessed it, merge step.
The merge step is that the solution to the straightforward problem of merging two sorted lists(arrays) to create one large sorted list(array).
The algorithm maintains three-pointers, one for every one of the 2 arrays and one for maintaining the present index of the ultimate sorted array.
Have we reached the top of any of the arrays? No: Compare current elements of both arrays Copy smaller element into a sorted array Move pointer of the element containing smaller element Yes: Copy all remaining elements of a non-empty array
 |
| merge sort algorithm steps |
Writing the Code for Merge Algorithm
A noticeable difference between the merging step we described above and therefore the one we use for merge sort is that we only perform the merge function on consecutive sub-arrays.
This is why we only need the array, the primary position, the last index of the primary subarray(we can calculate the primary index of the second subarray), and therefore the last index of the second subarray.
Our task is to merge two subarrays A[p..q] and A[q+1..r] to make a sorted array A[p..r]. therefore the inputs to the function are A, p, q and r
The merge function works as follows:
- Create copies of the subarrays L ← A[p..q] and M ← A[q+1..r].
- Create three-pointers i, j and k
b. j maintains a current index of M, starting at 1
c. k maintains the present index of A[p..q], starting at p.
- Until we reach the top of either L or M, pick the larger among the weather from L and M and place them within the correct position at A[p..q]
- once we run out of elements in either L or M, devour the remaining elements and put in A[p..q]
In code, this is able to look like:
// Merge two subarrays L and M into arr
void merge(int arr[], int p, int q, int r) {
// Create L ← A[p..q] and M ← A[q+1..r]
int n1 = q - p + 1;
int n2 = r - q;
int L[n1], M[n2];
for (int i = 0; i < n1; i++)
L[i] = arr[p + i];
for (int j = 0; j < n2; j++)
M[j] = arr[q + 1 + j];
// Handle the current index of sub-arrays and main array
int i, j, k;
i = 0;
j = 0;
k = p;
// follow these steps until we reach either end of either L or M, pick larger among
// elements L and M and place them within the correct position at A[p..r]
while (i < n1 && j < n2) {
if (L[i] <= M[j]) {
arr[k] = L[i];
i++;
} else {
arr[k] = M[j];
j++;
}
k++;
}
// When all the elements are end in either L or M,
// then take the remaining elements and put in A[p..r]
while (i < n1) {
arr[k] = L[i];
i++;
k++;
}
while (j < n2) {
arr[k] = M[j];
j++;
k++;
}
}
Merge( ) Function Explained Step-By-Step
A lot is occurring during this function, so let's take an example to ascertain how this is able to work.
As usual, an image speaks a thousand words.
 |
| mergesort algorithm |
The array A[0..5] contains two sorted subarrays A[0..3] and A[4..5]. allow us to see how the merge function will merge the 2 arrays.
void merge(int arr[], int p, int q, int r) {
// Here, p = 0, q = 4, r = 5 (size of array)Step 1: Create duplicate copies of sub-arrays to be sorted
// Create L ← A[p..q] and M ← A[q+1..r]
int n1 = q - p + 1 = 3 - 0 + 1 = 4;
int n2 = r - q = 5 - 3 = 2;
int L[4], M[2];
for (int i = 0; i < 4; i++)
L[i] = arr[p + i];
// L[0,1,2,3] = A[0,1,2,3] = [1,5,10,12]
for (int j = 0; j < 2; j++)
M[j] = arr[q + 1 + j];
// M[0,1,2,3] = A[4,5] = [6,9]
 |
| mergesort algorithm |
Step 2: Maintain a current index of sub-arrays and the main array
 |
| maintain copies of sub-array |
Step 3: Until we reach the top of either L or M, pick larger among elements L and M and place them within the correct position at A[p..r]
while (i < n1 && j < n2) {
if (L[i] <= M[j]) {
arr[k] = L[i]; i++;
}
else {
arr[k] = M[j];
j++;
}
k++;
}
 |
| mergesort algorithm |
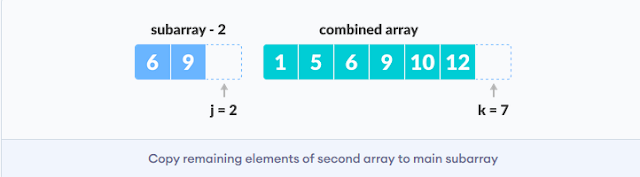
Step 4: once we run out of elements in either L or M, devour the remaining elements and put in A[p..r]
while (i < n1)
{
arr[k] = L[i];
i++;
k++;
}
 |
| Copy the remaining elements |
while (j < n2)
{
arr[k] = M[j];
j++;
k++;
}
}
 |
| mergesort in c |
This step would are needed if the dimensions of M were greater than L.
At the top of the merge function, the subarray A[p..r] is sorted.
Merge sort program in c: -
// Merge sort in C #include// Merge two subarrays L and M into arr void merge(int arr[], int p, int q, int r) { // Create L ← A[p..q] and M ← A[q+1..r] int n1 = q - p + 1; int n2 = r - q; int L[n1], M[n2]; for (int i = 0; i < n1; i++) L[i] = arr[p + i]; for (int j = 0; j < n2; j++) M[j] = arr[q + 1 + j]; // Maintain current index of sub-arrays and main array int i, j, k; i = 0; j = 0; k = p; // Until we reach either end of either L or M, pick larger among // elements L and M and place them in the correct position at A[p..r] while (i < n1 && j < n2) { if (L[i] <= M[j]) { arr[k] = L[i]; i++; } else { arr[k] = M[j]; j++; } k++; } // When we run out of elements in either L or M, // pick up the remaining elements and put in A[p..r] while (i < n1) { arr[k] = L[i]; i++; k++; } while (j < n2) { arr[k] = M[j]; j++; k++; } } // Divide the array into two subarrays, sort them and merge them void mergeSort(int arr[], int l, int r) { if (l < r) { // m is the point where the array is divided into two subarrays int m = l + (r - l) / 2; mergeSort(arr, l, m); mergeSort(arr, m + 1, r); // Merge the sorted subarrays merge(arr, l, m, r); } } // Print the array void printArray(int arr[], int size) { for (int i = 0; i < size; i++) printf("%d ", arr[i]); printf("\n"); } // Driver program int main() { int arr[] = {6, 5, 12, 10, 9, 1}; int size = sizeof(arr) / sizeof(arr[0]); mergeSort(arr, 0, size - 1); printf("Sorted array: \n"); printArray(arr, size); }
Merge Sort Complexity
Time Complexity- Best Case Complexity: O(n*log n)
- Worst Case Complexity: O(n*log n)
- Average Case Complexity: O(n*log n)
- Space Complexity
The space complexity of merge sort is O(n).
- Merge Sort Applications
- Inversion count problem
- External sorting
- E-commerce applications









No comments:
Post a Comment