Heap Sorting Algorithm
The heap sort algorithm is a arrangement and therefore the heaps are arrays of binary trees. Each node of the binary tree corresponds to a component of the array. Since a node has zero, one or two child nodes, for the i-th element of the array, the 2-th and (2i + 1) -th elements are its left and right children respectively.
The following figure shows an example of a heap during which the numbers in nodes are adequate to the orders in an array of 12 elements. the basis is that the first element of the array, and its left and right children are the second and third elements, respectively. The sixth element has just one child left and therefore the seventh doesn't .
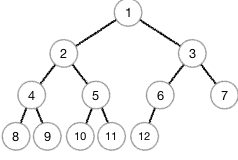
min heap
There are two sorts of heap: min-heap and max-heap. In min-heap parent nodes, nodes are smaller than child nodes (root node is that the smallest), while in max-heap it's opposite (root node is largest). we'll be using the max-heap property for Heapsort algorithm during this article.
Heapsort Algorithm
The strategy is as follows;
i) transform an array into a max heap;
ii) choose the basis , which is that the maximum number;
iii) keep the remaining array as a maximum heap;
iv) recurse ii) and iii).
Here is that the code from step iii) which is additionally utilized in step i). This "Max-Heapify" function takes two inputs: an array and an integer. The function compares the node during a given order (input integer) with its two children. If the node is smaller than either of the youngsters , it's swapped with the larger of the 2 child nodes.

Heap sort Algorithm
Although Max-Heapify doesn't exhaust the whole heap, by running the function on all nodes except leaves (the end nodes of the heap), we will turn any array into a max heap.

Heap sort
We are now able to implement Heapsort.
Heap sort algorithm
The following figure explains how Heapsort treats an array of 12 elements;
i) first, we turn the array into a max heap;
ii) take the basis , 12, and replace it with the last element,
3; iii) process Max-Heapify on the array of 11 elements remaining at the basis , and therefore the affected nodes are shown in dark blue; iii) recurse ii) and iii). within the end, we'll get an array sorted in ascending order. Heapsort works in situ , only storing a continuing amount of knowledge outside of the input array.

solution for Heap sort algorithm
heap sort time complexity
We can analyze the value of Heapsort by watching the sub-functions of Max-Heapify and Build-Max-Heap.
The cost of Max-Heapify is O (lgn). Comparing a node and its two child nodes costs Θ (1), and within the worst case, we rewind ⌊log₂n⌋ times down. Alternatively, the value of Max-Heapify are often expressed because the height h of the heap O (h).

heap sort time complexity
The cost of Build-Max-Heap is O (n). Since a heap of n elements features a depth of ⌊lgn⌋ and at any height there are ⌈n / 2ʰ⁺ ¹⌉ nodes except the leaves, we will derive the value as a complete of Max-Heapify O costs (h) shown left.
The total cost of Heapsort is O (nlgn), because it calls Build-Max-Heap (O (n)) and Max-Heapify (O (lgn)) over (n-1) times.
Check Performance For heap sort algorithm
The following table describes different sorting algorithms. needless to say , Heap sort algorithm follows other O (nlgn) cost algorithms, while it's not as cheap as Quicksort with a better constant hidden within the O notation.
While Heap sort doesn't beat Quick sort as a algorithm , Heap as a knowledge structure offers many various uses, and one among the foremost notable would be priority queues. With this Heap sort algorithm as an introduction to Heaps, we'll see how Heaps are applied to an efficient priority queue algorithm later.