Kruskel's algorithm

 This tutorial will help, you to find out about how Kruskel's algorithm works. Additionally, you'll find working samples of Kruskel's algorithm in C, C ++, Java, and Python.

Kruskel's algorithm is that the minimum spanning tree algorithm that takes a graph as input and finds a subset of the sides of that graph

 Form a tree that contains all the titles
 it's rock bottom weight among all the trees which will be formed from the graph
 

Understand working of Kruskel's algorithm

Greed belongs to the category of algorithms referred to as algorithms, which find the local optimal within the hope of finding a global optimal solution.

We start with rock bottom weight from the sides and continue adding edges until we reach our goal.

The steps for implementing Kruskell's algorithm are as follows:

•  Sort all edges from low to high
•  Take the sting with the smallest amount weight and fasten it to the wide tree. If adding a foothold creates a cycle, discard this edge.
•  Continue adding edges until all vertices are reached.
  

Kruskel's Algorithm Pseudocode

The Minimum Spanning Tree Algorithm is employed to see whether adding a foothold creates a loop or not.

The most common thanks to find this is often with the algorithm UnionFind. 

The union-find algorithm divides the vertices into clusters and allows us to see whether the 2 vertices belong to an equivalent cluster, so determine whether adding a foothold creates a cycle.

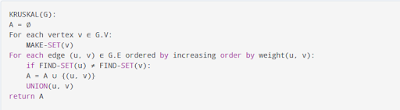Kruskel's Algorithm Pseudocode

Example of Kruskel's algorithm with solution

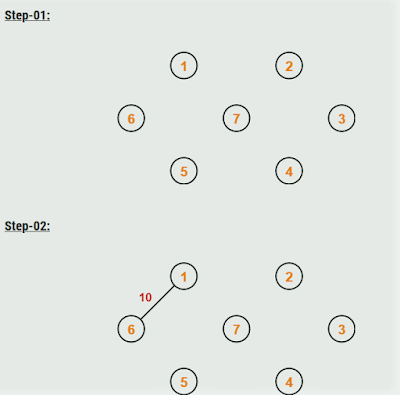
Step-01:

 Sort all the sides from low weight to high weight.

 
Step-02:

•  Take the sting with rock bottom weight and use it to attach the vertices of graph.
•  If adding a foothold creates a cycle, then reject that edge and choose subsequent least weight edge.

Step-03:

 Keep adding edges until all the vertices are connected and a Minimum Spanning Tree (MST) is obtained.

Minimum Spanning Tree Analysis-

•  the sides are maintained as min heap.
•  subsequent edge are often obtained in O(logE) time if graph has E edges.
•  Reconstruction of heap takes O(E) time.
•  So, Kruskal’s Algorithm takes O(ElogE) time.
•  the worth of E are often at the most O(V2).
•  So, O(logV) and O(logE) are same.

 
Special Case-

•  If the sides are already sorted, then there's no got to construct min heap.
•  So, deletion from min heap time is saved.
•  during this case, time complexity of Kruskal’s Algorithm = O(E + V) 

SOLVE PROBLEMS ON KRUSKAL’S ALGORITHM

SOLVE PROBLEMS

 Follow these steps to solve the problem

Steps to solve KRUSKAL’S ALGORITHM

 Now follow other two steps

Now follow other two steps

Step 5 and 6

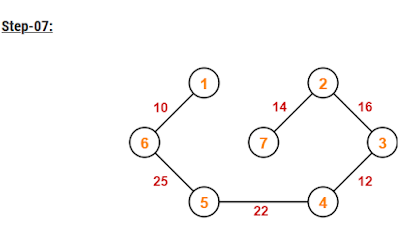Last Step 7

= 10 + 25 + 22 + 12 + 16 + 14

= 99 units

 Time Complexity for Kruskal’s Algorithm

Time Complexity for Kruskal’s Algorithm

C program for Kruskal’s Algorithm

#include <stdio.h>

#define MAX 30

typedef struct edge {
  int u, v, w;
} edge;

typedef struct edge_list {
  edge data[MAX];
  int n;
} edge_list;

edge_list elist;

int Graph[MAX][MAX], n;
edge_list spanlist;

void kruskalAlgo();
int find(int belongs[], int vertexno);
void applyUnion(int belongs[], int c1, int c2);
void sort();
void print();

// Applying Krushkal Algo
void kruskalAlgo() {
  int belongs[MAX], i, j, cno1, cno2;
  elist.n = 0;

  for (i = 1; i < n; i++)
    for (j = 0; j < i; j++) {
      if (Graph[i][j] != 0) {
        elist.data[elist.n].u = i;
        elist.data[elist.n].v = j;
        elist.data[elist.n].w = Graph[i][j];
        elist.n++;
      }
    }

  sort();

  for (i = 0; i < n; i++)
    belongs[i] = i;

  spanlist.n = 0;

  for (i = 0; i < elist.n; i++) {
    cno1 = find(belongs, elist.data[i].u);
    cno2 = find(belongs, elist.data[i].v);

    if (cno1 != cno2) {
      spanlist.data[spanlist.n] = elist.data[i];
      spanlist.n = spanlist.n + 1;
      applyUnion(belongs, cno1, cno2);
    }
  }
}

int find(int belongs[], int vertexno) {
  return (belongs[vertexno]);
}

void applyUnion(int belongs[], int c1, int c2) {
  int i;

  for (i = 0; i < n; i++)
    if (belongs[i] == c2)
      belongs[i] = c1;
}

// Sorting algo
void sort() {
  int i, j;
  edge temp;

  for (i = 1; i < elist.n; i++)
    for (j = 0; j < elist.n - 1; j++)
      if (elist.data[j].w > elist.data[j + 1].w) {
        temp = elist.data[j];
        elist.data[j] = elist.data[j + 1];
        elist.data[j + 1] = temp;
      }
}

// Printing the result
void print() {
  int i, cost = 0;

  for (i = 0; i < spanlist.n; i++) {
    printf("\n%d - %d : %d", spanlist.data[i].u, spanlist.data[i].v, spanlist.data[i].w);
    cost = cost + spanlist.data[i].w;
  }

  printf("\nSpanning tree cost: %d", cost);
}

int main() {
  int i, j, total_cost;

  n = 6;

  Graph[0][0] = 0;
  Graph[0][1] = 4;
  Graph[0][2] = 4;
  Graph[0][3] = 0;
  Graph[0][4] = 0;
  Graph[0][5] = 0;
  Graph[0][6] = 0;

  Graph[1][0] = 4;
  Graph[1][1] = 0;
  Graph[1][2] = 2;
  Graph[1][3] = 0;
  Graph[1][4] = 0;
  Graph[1][5] = 0;
  Graph[1][6] = 0;

  Graph[2][0] = 4;
  Graph[2][1] = 2;
  Graph[2][2] = 0;
  Graph[2][3] = 3;
  Graph[2][4] = 4;
  Graph[2][5] = 0;
  Graph[2][6] = 0;

  Graph[3][0] = 0;
  Graph[3][1] = 0;
  Graph[3][2] = 3;
  Graph[3][3] = 0;
  Graph[3][4] = 3;
  Graph[3][5] = 0;
  Graph[3][6] = 0;

  Graph[4][0] = 0;
  Graph[4][1] = 0;
  Graph[4][2] = 4;
  Graph[4][3] = 3;
  Graph[4][4] = 0;
  Graph[4][5] = 0;
  Graph[4][6] = 0;

  Graph[5][0] = 0;
  Graph[5][1] = 0;
  Graph[5][2] = 2;
  Graph[5][3] = 0;
  Graph[5][4] = 3;
  Graph[5][5] = 0;
  Graph[5][6] = 0;

  kruskalAlgo();
  print();
}