In this tutorial, you'll find out how sorting by binary search algorithm works. you'll also find practical samples of binary search in C, C ++, Java, and Python.

A binary search may be a search algorithm to seek out the position of a component during a sorted array.

In this approach, the element is usually searched for within the middle of a neighborhood of an array.

Binary search Algorithm working

The binary search algorithm is often implemented in two ways described below.

•  Iterative method
•  Recursive method

The recursive method follows the divide and conquer approach.

The general steps for both methods are described below.

•  The table during which the search should be performed is:

binary search in c

Let x = 4 be the element to look for.

• Set two pointers down and up respectively at rock bottom and highest positions.

Binary search algorithm

• Find the center element within the mid of the array, that is. (arr [low + high]) / 2 = 6.

binary search in C

• If x == mid, then returns mid.Else, compare the item to look for with m.

• If x> mid, compare x with the center element of the weather on the proper side of mid. this is often done by adjusting from low to low = medium + 1.

• Otherwise, compare x with the center element of the weather on the left side of the center. this is often done by setting high to high = medium - 1.

Binary search algorithm in data structure

• Repeat steps 3 through 6 until rock bottom meets the highest .

Mid element in binary search

• x = 4 is found.

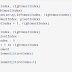
binary search program in c with Recursive Method

#include <stdio.h>

int binarySearch(int array[], int x, int low, int high) {
  if (high >= low) {
    int mid = low + (high - low) / 2;

    if (array[mid] == x)
      return mid;


    if (array[mid] > x)
      return binarySearch(array, x, low, mid - 1);

   
    return binarySearch(array, x, mid + 1, high);
  }

  return -1;
}

int main(void) {
  int array[] = {3, 4, 5, 6, 7, 8, 9};
  int n = sizeof(array) / sizeof(array[0]);
  int x = 4;
  int result = binarySearch(array, x, 0, n - 1);
  if (result == -1)
    printf("Not found");
  else
    printf("Element is found at index %d", result);
}

binary search program in c with Iterative Method

#include <stdio.h>

int binarySearch(int array[], int x, int low, int high) {
  // Repeat until the pointers low and high meet each other
  while (low <= high) {
    int mid = low + (high - low) / 2;

    if (array[mid] == x)
      return mid;

    if (array[mid] < x)
      low = mid + 1;

    else
      high = mid - 1;
  }

  return -1;
}

int main(void) {
  int array[] = {3, 4, 5, 6, 7, 8, 9};
  int n = sizeof(array) / sizeof(array[0]);
  int x = 4;
  int result = binarySearch(array, x, 0, n - 1);
  if (result == -1)
    printf("Not found");
  else
    printf("Element is found at index %d", result);
  return 0;
}

binary search Time Complexity

Time complexities

•  Best case complexity: O (1)
•  Average complexity of cases: O (log n)
•  Worst case complexity: O (log n)

Spatial complexity

The spatial complexity of the binary search is O (n).

Where We Use Binary Search Algorithm